En esta entrada voy a hablar de una implementación en PHP de un «Merkle Tree«, un árbol de Merkle, una implementación en árbol binario para conseguir un hash de un conjunto de datos. En anteriores artículos ya hablé de (o usé) árboles binarios, como en el artículo sobre la cola de prioridad en PHP (un buen ejemplo de árbol binario).
Esta estructura de datos fue originalmente propuesta en 1979 por Ralph Merkle, y de ahí su nombre.
Puedes ver la implementación de este Merkle Tree en mi github.
Usos más destacados
Los árboles de Merkle tienen una finalidad básica: obtener un hash, llamado Merkle Root, que identifique clara y unívocamente el conjunto original de datos. Por esta razón su uso está muy extendido en la comunicación entre ordenadores. A modo de ejemplo, cuando se descarga una gran cantidad de ficheros de un servidor podemos «calcular» si su contenido ha sido modificado/dañado comprobando que el Merkle Root original coincide con el que hemos calculado durante la descarga.
En el mundo de las criptomonedas también se aplica el algoritmo de Merkle Tree para comprobar que las transacciones no han sido modificadas. La primera criptomoneda del mundo, Bitcoin, incluye un Merkle Root en cada bloque.
Funcionamiento de un Merkle Tree
El funcionamiento de un árbol de Merkle es bastante simple. Se trata, en primer lugar, de asignar un hash a cada elemento del conjunto de datos. Cuando todos los datos estás hasheados, hay que concatenar esos mismo hashes y volver a aplicar la misma función de hash por parejas. Esta operación se repite hasta que sólo queda un nodo que, obviamente, contiene la raíz de Merkle.
Para mostrar gráficamente el funcionamiento, supongamos lo siguiente: hash(datos_1) = A, hash(datos_2) = B, … donde «datos_n» son cualquier conjunto de datos (cadena de texto, fichero, transacción, etc.).
Estos primeros valores hasheados suponen las «hojas» del árbol de Merkle a partir de los cuales vamos a construir la raíz de Merkle.
El hash sha256 de «A», como ya sabrás, es un valor de este estilo: 50ae61e841fac4e8f9e40baf2ad36ec868922ea48368c18f9535e47db56dd7fb
Obtenidas las hojas del árbol de Merkle, empezamos a «subir». Para cada par de nodos vamos a crear un «padre» que será el hash de la concatenación de los hashes de sus hijos. Si A = ‘abcdef’ y B = ‘123456’, entonces el padre de A y B es el hash resultante de ‘abcdef123456’. Veamos esto gráficamente:
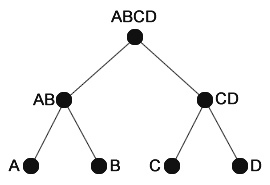
Merkle Tree para conjuntos de datos !^2
Pero no todos los conjuntos de datos son siempre potencias de 2. Podemos encontrar perfectamente un conjunto de datos que contenga 5 elementos, por ejemplo, A, B, C, D y E. Siempre que tengamos este caso tendremos que duplicar el elemento impar para obtener el hash del padre. Gráficamente se entiende mejor…
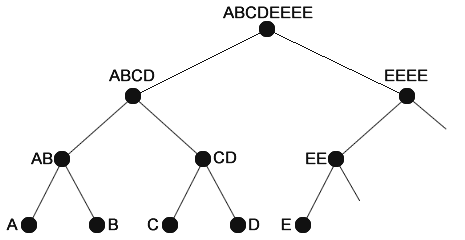
Como puedes ver, E no tiene hermano derecho. Para obtener al padre de E tenemos que duplicar a E y hashear normalmente. Así obtendremos el valor EE. Lo mismo pasa en el nivel superior. EE no tiene hermano derecho, por lo que procederemos a obtener al padre duplicando el hijo izquierdo y obteniendo EEEE.
Finalmente, ABCD sí tiene hermano derecho, nuestro reciente EEEE, así que hasheamos ambos valores obteniendo ABCDEEEE.
Como ves, acabamos de obtener un Merkle Root, con un número de elementos diferente de una potencia de dos, sin problemas.
Merkle Tree, Proof of Inclusion
Pero sin duda, lo más interesante de las raíces de Merkle es su «Proof of Inclusion«, prueba de inclusión.
La pregunta es: «¿Para qué sirve esto si no puedo comprobar que uno de mis datos forma parte del conjunto?». Pues por supuesto, podemos comprobar, y de forma muy eficiente [O(log n)], que un dato forma parte de la raíz de Merkle.
¿Cómo? Realmente es muy fácil. En la siguiente imagen se «busca» la prueba de inclusión del elemento K.

Fuente: Medium.com
Para probar la inclusión, sólo tendremos que obtener algunos hashes:
- HL
- HIJ
- HMNOP
- HABCDEFGH
Es fácil deducir lo siguiente:
- El hash de K se calcula y obtenemos HK
- El hash HKL se calcula con el hash HL
- El hash HIJKL se calcula a partir de HIJ y HKL
- El hash HIJKLMNOP se calcula a partir de HIJKL y HMNOP
- Y finalmente el Merkle Root se calcula a partir de HABCDEFGH y HIJKLMNOP
En resumen, sólo hemos necesitado 4 hashes para comprobar la inclusión del elemento K, entre 16 elementos!
Y si tuviéramos 5000 elementos, el coste sería sólo de 13 hashes!!! Sin duda, una invención genial.
Reflexiones finales
Como decía al principio, la Raíz de Merkle está presente en muchísimos algoritmos cotidianos sin que nos demos cuenta. El más conocido hoy, sin duda, es la descarga masiva de archivos, aunque las criptomonedas, y concretamente Bitcoin, también incluyen una raíz de Merkle.
El algoritmo de Merkle es realmente sencillo. Son las diferentes aplicaciones lo que hacen que sea realmente útil. Al final, como prácticamente todos los algoritmos conocidos, se trata de optimizar una determinada problemática en términos de computación, y desde luego que lo consigue.
¿Conocías este algoritmo?