Cola de prioridad en PHP 7.4

Hace unos días implementé una cola de prioridad en PHP 7.4 basándome en el concepto de ‘Heap‘. Un heap es un montón, una pila que parece desordenada, pero cuyo contenido sigue una lógica ordenada. De hecho, a partir de este concepto nace la técnica de ordenación del mismo nombre ‘Heap sort‘.

Antes de comentar la implementación de la cola, explicaré brevemente qué ventajas obtenemos al hacer así las cosas.

Ventajas de un heap para organizar una cola de prioridad

Al crear un sistema de prioridad como este buscamos obtener un medio ágil y rápido tanto de inserción como de extracción. En el caso del heap usamos un árbol binario, dado que con esta estructura podemos conseguir implementar la cola en un árbol (un array) homogéneo y completo. Este es el aspecto de un heap construido mediante un árbol binario:

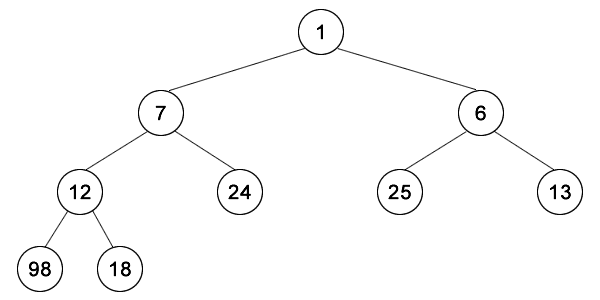
Como puedes ver, la prioridad de un padre siempre es mayor que la de sus hijos, sin importar demasiado las demás consideraciones.

En el caso del heap, el coste de las dos operaciones mencionadas es muy bajo; tanto en inserción como en extracción estamos hablando de un coste de «logaritmo en base 2 de N» en el peor de los casos, donde N es el número de elementos en la cola de prioridad. En notación Big O: O(log n).

Esto se explica mucho mejor con un ejemplo. Supongamos que tenemos una cola de 50 elementos. Si hacemos el cálculo, en el peor de los casos estamos introduciendo el elemento de mayor prioridad, y tendrá que ser «elevado» (up-heap) hasta la primera posición, lo que costaría 6 ejecuciones del bucle principal. El coste de inserción para 5.000 elementos sería de 12,3 ejecuciones y el de 500.000 elementos, 18,9. Interesante, ¿verdad?

Obviamente, si el elemento insertado no es el de máxima prioridad, el coste de inserción baja.

Operaciones básicas de una Cola de Prioridad en PHP

En una cola de prioridad se debe poder disponer, al menos, de las siguientes operaciones:

• push, insertar un elemento en la cola.
• pop, extraer el elemento de mayor prioridad de la cola.
• isEmpty, confirmación de que la cola está vacía.

Hay otras operaciones que son deseables en una cola de prioridad. Yo añado las siguientes:

• top, obtener el elemento de mayor prioridad, sin extraerlo de la cola.
• purge, eliminar todos los elementos de la cola.
• count, indicación del número de elementos existentes en la cola.
• print, imprimir la cola.

La implementación de las primeras dos operaciones las añado en pseudocódigo. En el futuro publicaré más artículos en los que usaré esta misma cola, siguiendo algunos puntos de lo que escribí en este artículo.

Implementación de la cola de prioridad

Vamos a ver cómo se implementan las tres operaciones principales mediante pseudo-código. Hablaremos básicamente de dos operaciones: 1) up-heap y 2) down-heap.

Insertar un elemento

Para insertar un elemento en la cola (up-heap) haremos lo siguiente:

1. Añadir el elemento al final del heap.
2. Comparar prioridad del nuevo elemento con su padre. Si es menor, paramos.
3. Si la prioridad es mayor, cambiar posiciones y volver al punto 2.

El término up-heap viene de su representación gráfica, ya que introducimos el nuevo elemento en la parte más baja del árbol, y lo vamos ‘elevando’ hasta su posición.

incrementar num_elementos_en_la_cola
siguiente_posicion = num_elementos_en_la_cola
posicion_padre = siguiente_posicion div 2

# Ejecutar la operación 'up-heap'
mientras (posicion_padre > 0) y
      (posicion_padre['prioridad'] > nuevo_elemento['prioridad'])
        cola[siguiente_posicion] = cola[posicion_padre]
        siguiente_posicion = posicion_padre
        posicion_padre = siguiente_posicion div 2
fmientras

# Colocar el nuevo elemento en su posición
cola[siguiente_posicion] = nuevo_elemento

Extraer un elemento

Para extraer un elemento haremos una operación muy similar a la anterior. En este caso vamos a tomar el último elemento del árbol binario (recuerda que es un array), y lo vamos a «bajar» desde la primera posición hasta la suya:

1. Poner el último elemento en el primer lugar del heap.
2. Comparar la prioridad con la de sus hijos. Si es mayor, paramos.
3. Si la prioridad es menor, cambiar posición con el primer hijo mayor y volver al paso 2.

Obviamente, el término down-heap también viene de su representación gráfica. Introducimos un elemento en la cúspide del árbol y lo vamos ‘bajando’ hasta su posición.

Si cola es vacía entonces
        lanzar excepción
Fsi

primer_elemento = cola[1]
ultimo_elemento = cola[num_elementos_en_la_cola]
Decrementar num_elementos_en_la_cola

primero = 1
hijo = primero * 2
Si (hijo existe y prioridad del hermano es mayor) entonces
        hijo = hijo + 1
Fsi

Mientras (hijo > num_elementos_en_la_cola) y 
      (cola[hijo]['prioridad'] < ultimo_elemento['prioridad'])   
        cola[primero] = cola[hijo]
        primero = hijo
        hijo = primero * 2
        //Otra vez miramos la prioridad de los hijos
        Si (hijo existe y prioridad hermano es mayor) entonces
                hijo = hijo + 1
        Fsi
Fmientras

cola[primero] = ultimo_elemento

retornar primer_elemento

Cola vacía

Es posible que intentemos obtener un elemento de una cola vacía, y esto generaría un error en la aplicación. Para ello debemos tener un método que indique si la cola está vacía o no.

En nuestra implementación, esto es muy fácil. Sólo tenemos que comprobar que el número de elementos es 0. Devolvemos un valor booleano en la función isEmpty que implementamos de la siguiente manera:

return num_elementos_en_la_cola == 0

Más fácil imposible…

Código fuente

Ver pseudocódigo está muy bien, pero a muchos nos gusta poder probar el código, o incluso ver cómo evoluciona con un debugger.

El código fuente de esta cola de prioridad está disponible en mi GitHub: Cola de prioridad en PHP.

Y por supuesto, si te ha gustado mi código y quieres comprarme un café, aquí te lo pongo fácil. 😉